
 |
|||||
8. Динамическое поле покоя-движения в равномерном круговом движении
Л. Г. Крейдик
В покое-движении по окружности радиуса а состояние материальной точки m определяется параметром
![]() ,
(8.1)
,
(8.1)
где составляющие состояния в неподвижном и подвижном базисах соответственно равны:
![]() ,
,
![]() .
(8.1а)
.
(8.1а)
![]() ,
,
![]() . (8.1b)
. (8.1b)
Состояние точки выражается также
произведением потенциально-кинетической массы точки на радиус окружности:
![]() .
Потенциально-кинетическая масса точки имеет вид:
.
Потенциально-кинетическая масса точки имеет вид:
![]() ,
(8.2)
,
(8.2)
где потенциальная и кинетическая масса в неподвижном и подвижном базисах соответственно равна:
![]() ,
,
![]() (8.2а)
(8.2а)
![]() ,
,
![]() . (8.2b)
. (8.2b)
Потенциальная вращательная масса - продольная, радиальная центростремительная масса; кинетическая вращательная масса - поперечная, тангенциальная центробежная масса.
Потенциально-кинетический импульс точки в круговом движении выражается формами:
![]() ,
(8.2)
,
(8.2)
где
![]() (8.2а)
(8.2а)
- потенциально-кинетическая, продольно-поперечная, центростремительно-центробежная, радиально-тангенциальная скорость покоя-движения, определяющая соответствующие импульсы:
![]() ,
(8.2а)
,
(8.2а)
![]() .
(8.2b)
.
(8.2b)
Скорость изменения состояния массы, или заряд, носит потенциально-кинетический характер и имеет вид :
![]() .
(8.3)
.
(8.3)
В неподвижном базисе потенциальный и кинетический заряды соответственно равны:
![]() ,
,
![]() . (8.3а)
. (8.3а)
В подвижном базисе имеем:
![]() ,
,
![]() . (8.3b)
. (8.3b)
Потенциальный заряд описывает радиальное центростремительное поле покоя, кинетический заряд - тангенциальное центробежное поле движения.
Потенциально-кинетический импульс, как момент заряда, описывается равенствами:
![]() .
(8.4)
.
(8.4)
Потенциально-кинетический импульс представляется взаимно перпендикулярными импульсами покоя и движения, что отражает ортогональность этих полей.
Кинема поля изменения импульса описывает обмен покоем-движением и выражается следующими равносильными формами:
![]() ,
(8.5)
,
(8.5)
![]() ,
(8.5а)
,
(8.5а)
![]() ,
(8.5b)
,
(8.5b)
![]() ,
(8.5c)
,
(8.5c)
где ![]() - потенциально-кинетический продольно-поперечный
центростремительно-центробежный ток:
- потенциально-кинетический продольно-поперечный
центростремительно-центробежный ток:
![]() .
(8.6)
.
(8.6)
Потенциальный продольный (радиальный)
центростремительный ток покоя ![]() и кинетический поперечный (тангенциальный) центробежный ток движения
и кинетический поперечный (тангенциальный) центробежный ток движения ![]() в неподвижном и подвижном базисах имеют вид:
в неподвижном и подвижном базисах имеют вид:
![]() ,
,
![]() , (8.6а)
, (8.6а)
![]() ,
,
![]() . (8.6b)
. (8.6b)
Итак, в поле кругового покоя-движения кинема является продольно-поперечным радиально-тангенциальным параметром обмена покоем-движением:
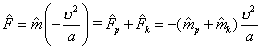 ,
(8.7)
,
(8.7)
или
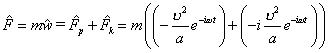 .
(8.8)
.
(8.8)
Потенциальная продольная (радиальная) центростремительная кинема обмена покоем имеет формы:
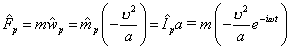 .
(8.8а)
.
(8.8а)
Подобные формы имеет кинетическая поперечная (тангенциальная) центробежная кинема обмена движением:
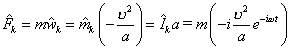 .
(8.8b)
.
(8.8b)
В подвижном базисе потенциально-кинетическая, центростремительно-центробежная кинема имеет вид:
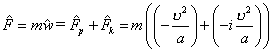 .
(8.8c)
.
(8.8c)
Если опираться на удельное потенциально-кинетическое ускорение, кинему обмена покоем-движением можно представить так:
![]() .
(8.8d)
.
(8.8d)
Рассмотрим еще одну важную форму
кинемы обмена, которую получим, преобразую
форму (8.8): ![]() .
Если кинематическую скорость обозначить через B,
тогда кинема представиться следующей формой:
.
Если кинематическую скорость обозначить через B,
тогда кинема представиться следующей формой:
![]() .
(8.8е)
.
(8.8е)
Если ![]() - заряд надстройки, а нас интересует заряд базиса, тогда согласно (4.33) получаем
кинему вида
- заряд надстройки, а нас интересует заряд базиса, тогда согласно (4.33) получаем
кинему вида
![]() .
(8.8f)
.
(8.8f)
В поперечном поле обмена, эта формула носит название силы Лоренца.
С импульсом и кинемой связаны соответствующие потенциально-кинетические моменты:
а) потенциально-кинетический продольно-поперечный центростремительно-центробежный момент импульса покоя-движения
![]() ,
(8.9)
,
(8.9)
где ![]() - момент инерции в круговом движении;
- момент инерции в круговом движении;
![]() (8.9а)
(8.9а)
- кинетический тангенциальный центробежный момент импульса;
![]() (8.9b)
(8.9b)
- потенциальный радиальный центростремительный момент импульса.
б) потенциально-кинетический продольно-поперечный центростремительно-центробежный момент кинемы покоя-движения
![]() .
(8.10)
.
(8.10)
Продольный (радиальный) центростремительный потенциальный момент и поперечный (тангенциальный) центробежный кинетический момент в неподвижном и подвижном базисах определяются выражениями:
![]() ,
,
![]() (8.10а)
(8.10а)
![]() ,
,
![]() . (8.10b)
. (8.10b)
Отношение момента заряда ![]() к моменту импульса
к моменту импульса ![]() имеет вид:
имеет вид:
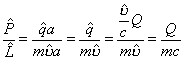 (8. 11)
(8. 11)
Потенциально-кинетическая продольно-поперечная энергия покоя-движения точки по окружности определяется интегралом:
![]() ,
(8.12)
,
(8.12)
при этом
![]() ,
(8.12а)
,
(8.12а)
и полная мера энергии по окружности есть мера вида:
![]() .
(8.12b)
.
(8.12b)
Разность кинетической и потенциальных энергий в подвижном базисе определяет модуль энергии:
![]() .
(8.12с)
.
(8.12с)
Итак, при движении по окружности (как это в частности имеет место в Н-атоме) потенциальная и кинетическая энергии материальной точки взаимно уравновешены.
В силу этого круговое движение является оптимальным (равновесным) состоянием поля покоя-движения, при котором “притяжение” и “отталкивание” взаимно уравновешиваются, что обеспечивает устойчивость орбитального движения в микро- и мега мире. Квантитативное равенство “притяжения” и “отталкивания” одновременно сопровождается квалитативным неравенством направлений полей покоя и движения, что и порождает вечное круговое волновое движение. Для того чтобы оно исчезло нужно разрушить полностью эту систему, но и тогда возникнет большое число новых круговых волновых движений, более дисперсных уровней.
Если радиус окружности стремиться к бесконечности, любой участок окружности можно рассматривать как прямолинейное движение-покой. Сумма кинетической и потенциальной энергий такого “прямолинейного” движения, как и в круговом движении, равна нулю, но модуль не равен нулю.
Все изложенные понятия теоретической философии необходимы для реалистического описания физических полей.

Copyright © Л.Г.Крейдик , 2001-2005