10. Kinematic-dynamic exchange of a system with environment. Charges of an exchange

	Main page	Contents of issue B-02	E-mail to author	Previous page	Next page

10. Kinematic-Dynamic Exchange of a system with environment

L. G. Kreidik (translation from Russian T. S. Kortneva and G. P. Shpenkov)

10.1. -level exchange

We will consider dynamic-kinematic exchange of a system with the environment on the P-level represented in Fig. 2.13 by a graph of exchange.

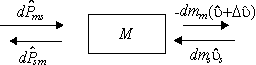
Fig. 2.13. A graph of -level exchange.

Kinematic variation in the momentum of the system is

, (2.236)

where is the partial kinematic momentum transferred from the environment, is the partial kinematic momentum transferred by the system to the environment.

Dynamic variation of the momentum is

, (2.237)

where is partial dynamic momentum transferred from the environment, is partial dynamic momentum transferred by the system to the environment; is the velocity of mass ; is the velocity of the system; is a discrete jump of the velocity.

The resultant transfer is

, (2.238)

and

, (2.239)

where is the kinematic kinema, and are dynamic mass charges.

Since the total rate of change of momentum is

, and , (2.240)

expression (2.239) can be written as

(2.241)

-- , (2.241a)

where e is a discrete derivative, describing the jump of the velocity,

In steady-state dynamic exchange, we have

, , (2.242)

, (2.243)

where is an effective velocity which we will call the vector of field strength of rest-motion in dynamic exchange.

When dynamic exchange prevail, we have

. (2.244)

This formula is, however, valid for kinematic exchange as well, if q is meant as a kinematic charge modulus.

10.2. Field Strengths of Rest-Motion

The effective potential and kinetic field velocities strengths of circular motion will be determined from formulas (2.184)-(2.186) and (2.244):

, (2.245)

. (2.246)

The axial field strength has the form

. (2.247)

The potential field strength describes the Yes-subfield, the kinetic field strength, the No-subfield; and the axial field strength describes the Yes-No subfield of the circular motion-rest field.

If motion is uniform,

, (2.248)

, (2.249)

. (2.250)

The total energy of the fields of all three levels of rest-motion of the system with mass m is:

. (2.251)

The energy structure of this motion-rest field is shown in Fig. 2.14.

Fig. 2.14.A graqph of energies

Motion of a material point with the charge q in the field of circular rest-motion,characterized by vectors , and , can be expressed in the form:

, , . (2.252)

Such structure is valid for any level of motion-rest because the ratio of charge to mass of a moving object (motator) defines an effective field frequency

, (2.253)

Its fundamental wavelength will be

, (2.254)

where c is the wave velocity of the field.

We will supplement these equations by simple relations between the oscillation amplitude a, oscillation velocity u , wavelength l , and the wave velocity c:

and , (2.255)

where

(2.256)

is a wave radius.

The similar correlation between the local E and wave A velocities-strengths of the motion-rest field

(2.257)

follows from the last relations.

The same relation also holds between the local and wave moments of charge:

, (2.258)

where is a local moment and is a wave moment.

It is evident that the relation between the local moment of charge and the wave moment of momentum has the form

(2.259)

On the basis of formula (2.257), all three vector equations of motion in (2.252) can be expressed by a general equation

. (2.260)

Since and , then

or . (2.261)

One can see from the above equation that when the field strength A approaches the wave velocity c, the specific velocity w tends to the limiting fundamental frequency w _c of the field.